알고리즘을 짤 때 분할정복 기법을 사용하는 경우가 많습니다. 큰 문제를 한 번에 해결하기 힘들 때 작은 여러 개의 문제로 나누어서 푸는 기법인데요. 작은 문제들을 풀다보면 같은 문제들을 반복해서 푸는 경우가 생깁니다. 그 문제들을 매번 재계산하지 않고 값을 저장해두었다가 재사용하는 기법이 동적 프로그래밍입니다.
대표적인 문제 세 가지 : 막대기 자르기, 최장 공통 부분 수열, 0/1 배낭
1. 막대기 자르기
일단 막대기부터 잘라봅시다. 하나의 긴 막대기가 있는데 막대기 조각마다 가격이 다릅니다. 막대기를 적절하게 잘라서 가장 가격이 높게 만들어야 합니다.
길이(i) 0 1 2 3 4 5 6 7 8 9 10
가격(Pi) 0 1 5 8 9 10 17 17 20 24 30
예를 들면 길이가 4인 막대기를 자를 때 얻을 수 있는 최대 가격은, 길이를 2인 막대기 두 개로 나누어서 가격을 5 + 5 = 10으로 만드는 겁니다. 길이가 6인 막대는 자르지 않고 그냥 팔았을 때 최대 17의 가격을 얻을 수 있습니다.
이 문제는 그냥 풀기엔 좀 복잡하게 보이지만 동적 프로그래밍을 사용하면 간단하게 풀 수 있습니다.
길이가 n인 막대기의 최대 가격을 Rn이라고 했을 때, Rn = max(Pi + Rn-i) (i는 1부터 n)로 나타낼 수 있습니다. max는 여러 값 중의 최대값을 의미합니다. 예를 들면 아까 길이가 4인 막대기의 최대 가격은 R4 = max(P1 + R3, P2 + R2, P3 + R1, P4 + R0)이죠.
P1, P2, P3은 이미 주어져 있습니다. 이제 R1, R2, R3을 구해야 하는데요.
R1은 Rn = max(Pi + Rn-i) (i는 1부터 n) 식에서 max(Pi + R0)이므로 1입니다.
R2는 max(P1 + R1, P2 + R0)이라 max(2, 5) = 5입니다.
R3는 max(P1 + R2, P2 + R1, P3 + R0)라서 max(6, 6, 8) = 8입니다.
R4는 위의 값들로부터 max(9, 10, 9, 9) = 10임을 알 수 있습니다.
위의 과정에서 R1, R2, R3는 계속해서 나옵니다. 이 값들을 저장해 두고 재사용하면 일일히 재계산하지 않아도 되죠. 바로 여기서 Top-down으로 불리는 메모이제이션을 사용할 수도 있고, Bottom-up이라 불리는 상향식 계산법을 사용할 수도 있습니다.
[메모이제이션이란]
꼬리재귀(피보나치 수열 계산)처럼 한 번 계산한 값들을 저장해두고 재사용하는 방법을 말합니다.
int dp(vector<int> P, n)
{
vector<int> R(n);
for (int i = 0; i < n; i++)
{
int temp = -1;
for (int j = 0; j < i; j++)
{
temp = max(temp, p[i] + r[j - i]);
}
r[i] = temp;
}
return r[n];
}
2. 최장 공통 부분 수열
최장 공통 부분 수열(LCS) 문제는 두 개의 문자열에서 순서대로 겹치는 문자가 최대 몇 개인지 구하는 문제입니다. 예를 들어 ABCBDAB와 BDCABA에서 LCS는 BCAB나 BDAB나 BCBA입니다. 앞에서부터 겹치는 것들을 찾아서 문자열을 만들 때 그것이 가장 길다면 LCS가 되는 거죠.
이 문제는 다음과 같이 분석할 수 있습니다. i라는 문자열과 j라는 문자열이 있다고 칩시다. lcs(i,j)는 이 두 문자열의 LCS 길이입니다. 만약 문자열의 마지막 두 문자가 같다면 lcs(i, j) = lcs(i-1, j-1) + 1과 같습니다. lcs(ABCBDAB, BDCAB)는 lcs(ABCBDA, BDCA) + 1과 같은 거죠.
만약 두 문자열의 마지막 문자가 다르다면, lcs(i, j) = max(lcs(i, j-1), lcs(i -1, j))가 됩니다. lcs(ABCBDAB, BDCABA)는 lcs(ABCBDA, BDCABA)와 c(ABCBDAB, DBCAB) 중 더 큰 값이 되는 겁니다.
이렇게 끝부분부터 비교해 하나씩 줄여가면 LCS의 길이가 나오게 됩니다.
#include <cstdio>
#include <cstring>
#include <algorithm>
char str1[1010];
char str2[1010];
int LCS[1010][1010];
int main()
{
scanf("%s", &str1);
scanf("%s", &str2);
int s1 = strlen(str1);
int s2 = strlen(str2);
for (int i = 1; i <= s1; i++) {
for (int j = 1; j <= s2; j++) {
if (str1[i - 1] == str2[j - 1])
LCS[i][j] = LCS[i - 1][j - 1] + 1;
else
LCS[i][j] = std::max(LCS[i - 1][j], LCS[i][j - 1]);
}
}
printf("%d\n", LCS[s1][s2]);
return 0;
}
3. 0/1 배낭
배낭 문제는 무게 제한이 50인 배낭에 다음과 같은 세 개의 물건을 넣는 문제입니다. 넣은 물건들의 가치(v) 합이 최대가 되면 됩니다. 문제는 세 물건의 무게(w)를 합치면 60이라 다 넣지는 못한다는 겁니다.
이 문제 이름이 0/1인 이유는 물건을 쪼개서 넣지는 못하고, 선택지가 통째로 넣거나 아예 안 넣거나 두 개밖에 없기 때문입니다.
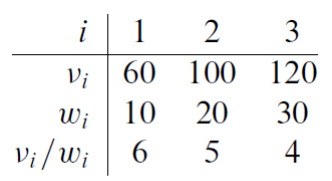
직관적으로 보면 2번과 3번 물건을 넣어서 무게는 50으로 맞추고, 가치는 220으로 하면 최적입니다. 문제는 컴퓨터한테 이 문제를 어떻게 풀도록 하냐는 거죠. 컴퓨터에게는 직관이 없습니다.
제일 먼저 떠오르는 것은 무게 대비 가치 순서로 고르도록 하는 겁니다. 이렇게 하면 1번과 2번을 선택하게 되고, 3번을 선택하지 못합니다. 틀린 결과죠.
사실 방법은 없습니다. 그냥 모든 경우를 계산해서 노가다로 푸는 겁니다. 중간에 계산 결과가 겹치는 부분은 저장해서 재사용하고요.